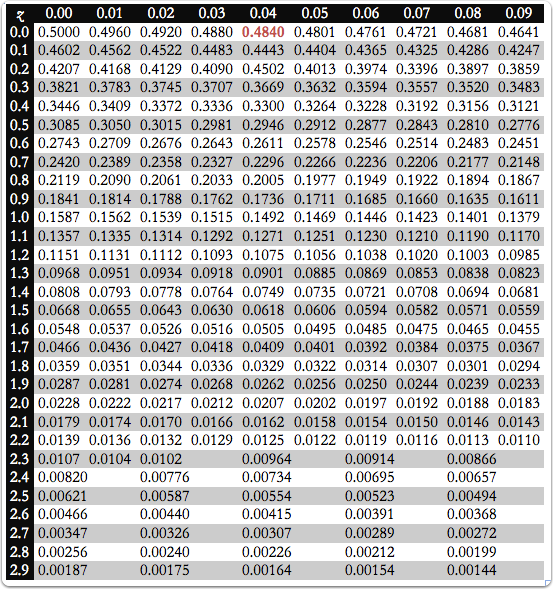
The table below gives the proportion, \(P\), of the area under a normal distribution curve that lies to the right of a deviation, \(z\), which is defined as
where \(\mu\) and \(\sigma\) are the distribution’s mean and standard deviation, respectively, and where \(x\) is the value for which the deviation is defined. For example, the area under a normal distribution to the right of a deviation of +0.04 is 0.4840 (see entry in red), or 48.40% of the total area. The area to the left of the deviation is \(1-P\). For a deviation of +0.04, this is 1 – 0.4840, or 51.60%. If \(x\) is smaller than \(\mu\), then \(z\) is negative. In this case, the values in the table give the area to the left of \(z\). For example, if \(z\) is –0.04, then 48.40% of the area lies to the left of the deviation.
To use the single-sided normal distribution table, sketch the normal distribution curve for your problem and shade the area that corresponds to your answer. This divides the normal distribution curve into three regions: the shaded area that corresponds to your answer, the area to the right of this, and the area to the left of this. Calculate the values of \(z\) for the limits of the area that corresponds to your answer. Use the table to find the areas to the right and to the left of these deviations, subtract these values from 100% and, voilà, you have your answer.

A pdf copy of this appendix is available using this link.