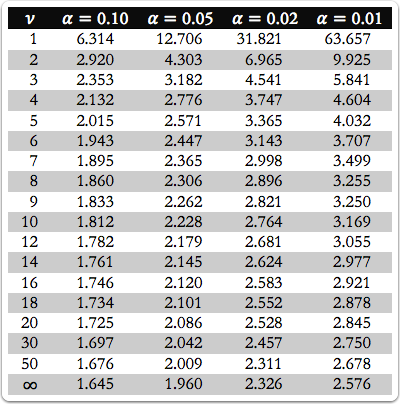
The table below gives values of \(t\left( \alpha ,\nu \right) \) where \(\alpha\) defines the confidence level and \(\nu\) defines the degrees of freedom. Values for \(\alpha\) are defined as follows
\(\alpha\) = 1 - confidence level (as fraction)
For example, for a 95% confidence level, \(\alpha =1-0.95=0.05\). The degrees of freedom is the number of independent measurements given any constraints that we place on the measurements. For example, if we have \(n\) measurements and we calculate their mean, \(\overline { x } \), then we have \(n-1\) degrees of freedom because the mean, \(\overline { x } \), and the values for the first four measurements, \({ x }_{ 1 }\), \({ x }_{ 2 }\), \({ x }_{ 3 }\), and \({ x }_{ 4 }\), removes the independence of the fifth measurement, \({ x }_{ 5 }\), whose value is defined exactly as
The values of \(t\) in this table are two-tailed in that they define a confidence interval that is symmetrical around the mean. For example, for a 95% confidence interval (\(\alpha=0.05\)), half of the area not included within the confidence interval is at the far right of the distribution and half is at the far left of the distribution. For a one-tailed confidence interval, in which the excluded area is on one side of the distribution, divide the values of \(\alpha\) in half; thus, for a one-tailed 95% confidence interval, we use values of \(t\) from the column where \(\alpha=0.1\).

A pdf copy of this appendix is available using this link.